In my previous post, I focused on the translational mass dampers as one of the strategies for active control of vibrations in tall structures. Today, let’s explore a semi-active control using a different type of mass dampers – the magnetorheological ones.
What is a magnetorheological damper?
A magnetorheological (MR) damper is a device filled with fluid, which increases its viscosity when subjected to a magnetic field. Varying the magnetic field intensity, the viscosity of the fluid and its ability to transmit force can be controlled fairly accurately. This type of shock absorbing and damping control found use in many applications, especially in semi-active vehicle suspensions.
In the past 20 years, the magnetorheological dampers attracted a lot of interest in structural engineering as well. Being relatively low-cost, with low power requirements, these semi-active dampers can effectively mitigate deflection in structures. Another advantage of the MR dampers is that they can function in both active (controlled by the electromagnet) and passive modes (as an ordinary liquid damper). They offer a ‘natural’ fail-safe feature when the active damping cannot be engaged, for example, due to a power outage.
Modeling magnetorheological dampers
To use MR dampers effectively, you need to design a control system using an accurate mathematical model that represents their dynamics. But with their extremely nonlinear characteristics, MR dampers are notoriously difficult to model. Many researchers became interested in this area. They started to investigate and validate different methods for identifying the model of the MR dampers to determine new, effective methods in damping the structures’ vibrations.
Clipped-optimal control for magnetorheological dampers
A great example of such research is the paper Modeling and Control of Magnetorheological Dampers for Seismic Response Reduction. The team led by Dr. Shirley Dyke published their work in the journal Smart Material and Structures in 1996. The team used a prototype MR damper from Lord Corporation that could potentially be used in active control of actual structures.
In the passive mode, when no voltage is applied, the MR damper behaves like any ordinary damper. That means it could be modeled using a linear viscous friction model. However, when a magnetic field is applied, the fluid inside the damper becomes stiffer and provides more damping. This effect can be characterized by the mechanical model shown in the figure below. The Bouc-Wen hysteresis element is needed to obtain an accurate mathematical representation of an MR damper.
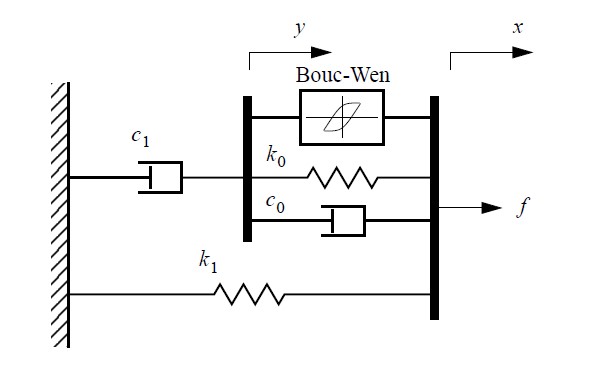
Using this model, the researchers characterized the MR damper with a set of eight equations. To identify parameters in these equations, they applied a constrained nonlinear optimization method. To validate the accuracy of their model, they compared its simulation response with the measured response of the actual MR damper hardware.
Validation on a seismic simulator
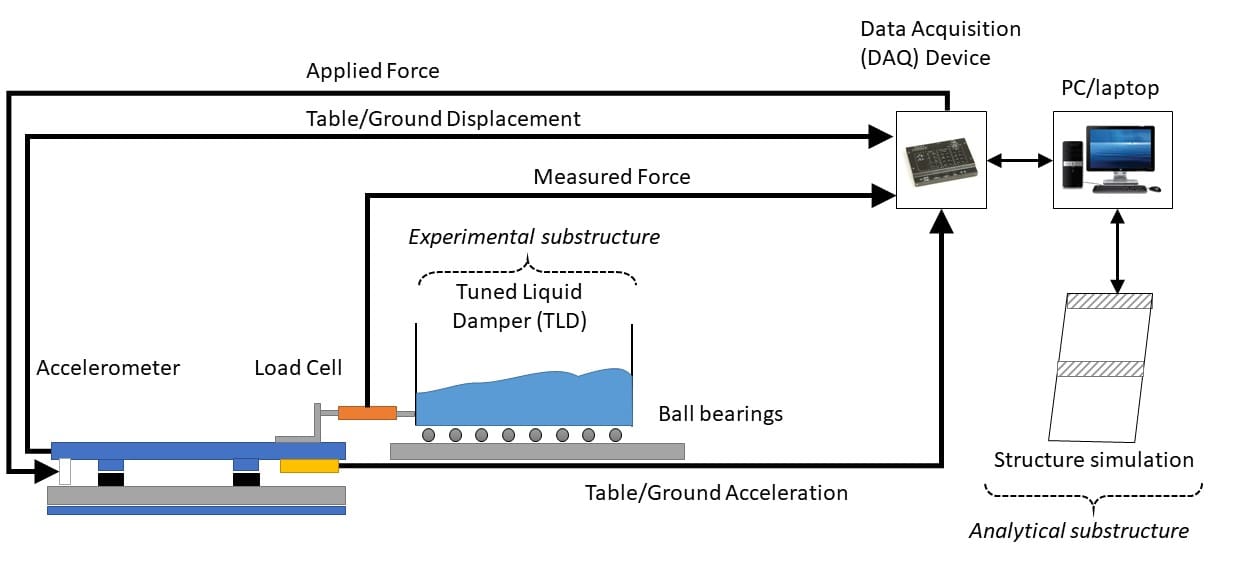
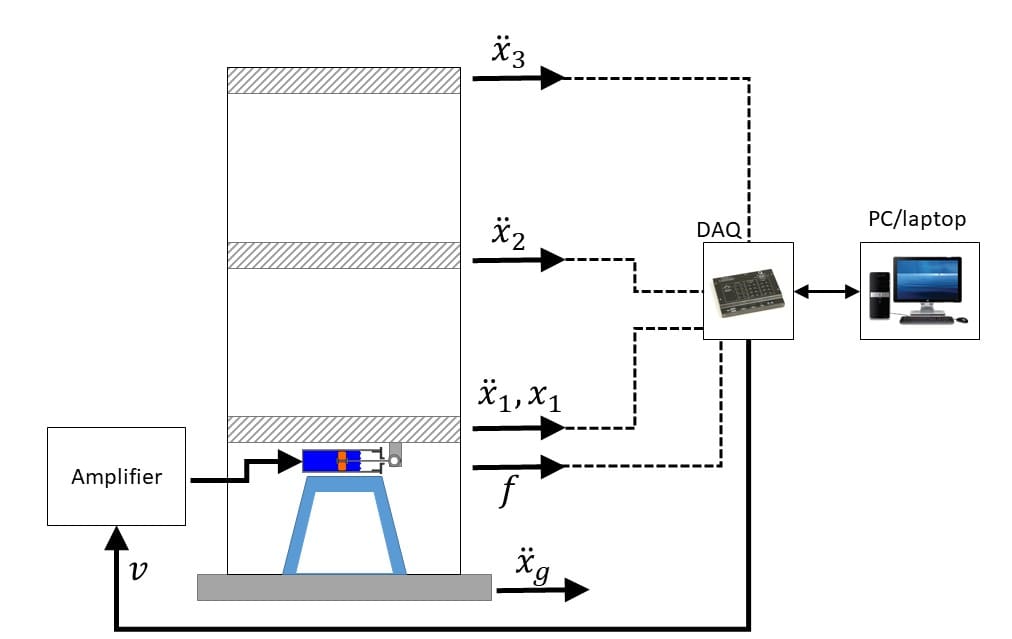
Once they validated the mathematical model, the researchers designed a clipped-optimal controller for the active damping control of a structure. This schematic shows how the shake table and structure interface to the PC, data acquisition device, and MR damper:
The next figure shows a high-level block diagram of the clipped-optimal control developed by the team:
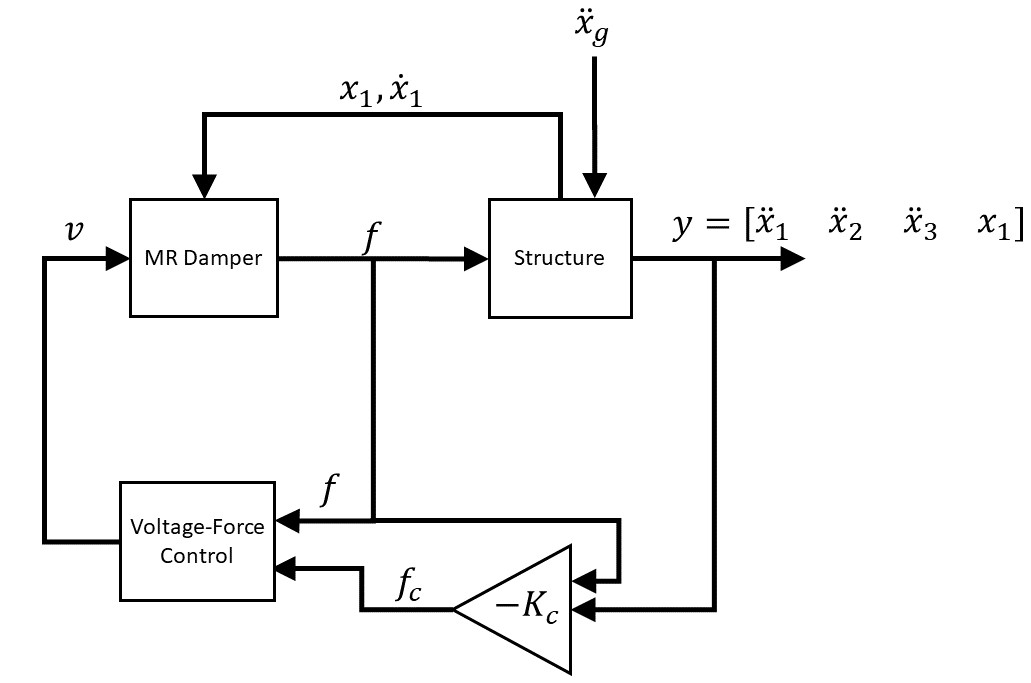
To confirm the validity of their model and the control approach, the researchers fitted the MR damper on a three-story test structure. They exposed the structure to a scaled-down earthquake motion on a Quanser Shake Table II seismic simulator, using a Quanser data acquisition device to run the shake table, apply a voltage to the MR damper, and measure its corresponding force output. They compared the performance of the uncontrolled structure to passive damping (when no voltage is applied) and clipped-optimal control.
The passive mode alone helped a great deal. It reduced the displacement by 52.7% and the acceleration of the top floor by 48.8%. The clipped-optimal control further improved the performance, successfully attenuating the top floor motions by an additional 25.3%.
The research continues
Since the publication of their work on clipped-optimal control, Dr. Shirley Dyke and her team have done more research in this domain by using the technique on larger scaled systems. There are other many examples of work on modeling and identification of magnetorheological dampers. So, if you are interested in the topic, there are other works you can examine. The team from the Polytechnic University of Catalonia, University of Girona, and University of Bristol published their research on modeling and identification of a small-scale magnetorheological damper in the Journal of Intelligent Material Systems and Structures, 2008 and presented it at the 10th IFAC Workshop on the Adaptation and Learning in Control and Signal Processing in 2010. The researchers from the University of Western Sydney and Harbin Institute of Technology published the paper Modeling and dynamical performance of the electromagnetic mass driver system for structural vibration control in the Journal of Engineering Structures, 2015.
And if you focus on studying similar problems, share your work with us. Add a comment and let us know what you are working on.